Лучшие нейросети для математики: решаем задачи ЕГЭ и олимпиад за считаные минуты

Подготовка к экзамену или олимпиаде по математике – сложный процесс, на котором легко «споткнуться». Ученик вроде понимает условие задачи, начинает ее решать и на каком-то этапе застревает: не сходится ответ, неясно, где произошла ошибка, ускользает логика решения.

Здесь на помощь может прийти нейросеть для математики. Она не окажется полноценной заменой ученику – не будет думать за него, да и на экзамене воспользоваться ИИ было бы сложно. Однако современные умные модели могут стать удобными тренажерами, инструментами, объясняющими непростые для понимания правила и формулы.

Из этой статьи вы узнаете, как можно использовать нейросети при подготовке к ЕГЭ и олимпиадам по математике, как составлять промпты и как популярные ИИ-модели справляются с ролью онлайн-репетитора. Тесты проводились на базе нейросетей, доступных в агрегаторе GPTunneL.

Как правильно использовать нейросеть для задач по математике

Если относиться к ИИ как к автоматическому генератору ответов, он быстро начнет вредить: будет давать правильный результат, но не поможет понять сложную тему. Рабочий подход – использовать нейросеть в трех аспектах:

1. Объяснение: просите пошаговый разбор решения, с пояснением каждого действия и кратким выводом, почему произведено именно это действие. Добавьте роль: «объясни как учитель, но без лишней воды», тогда ответы будут развернутыми, но по существу.
2. Проверка: загружаете в ИИ-модель собственное решение, просите найти неправильное действие, исправить алгоритм и объяснить, как должно быть.
3. Тренажер: просите нейросеть сгенерировать 10 задач этого же типа с кратким описанием решений и ответов. Заранее уточняйте уровень сложности, меняйте его при необходимости. Так вы разнообразите собственный пул практических навыков.

Но всегда помните: опасно, если модель:

• Отвечает слишком быстро и без описания шагов;
• Не преобразует значения («очевидно, что…»);
• Не проверяет область допустимых значений и отбор корней.

Поэтому перепроверка каждого ответа – это база, которую не стоит игнорировать.

Типовые задачи ЕГЭ: разбор и универсальные промпты для тренировки

Алгебра

Мини-задача: «Решите уравнение |2x − 3| = x + 5».

Типичная ошибка здесь – забыть про ОДЗ (правая часть должна быть неотрицательной) и не проверить корни подстановкой.

Алгоритм решения всегда один: ограничения → разбор по случаям → проверка. Вот три универсальных промпта, которые следуют этому алгоритму:

• Промпт для объясния решения по шагам: «Реши уравнение |2x − 3| = x + 5. Сначала выпиши ОДЗ, затем реши по случаям. Каждый шаг расписывай подробно. Все найденные корни обязательно проверь подстановкой. В конце кратко поясни метод решения».
• Промпт для поиска поиска ошибки в решении: «Я решал(а) уравнение |2x − 3| = x + 5. Найди первый неверный шаг, объясни ошибку и исправь решение. Проверь итоговый ответ подстановкой. Мое решение: [вставь свой текст]».
• Промпт для генерации 10 похожих задач: «Сгенерируй 10 задач уровня ЕГЭ на уравнения с модулем |ax + b| = cx + d. Для каждой задачи дай ответ и короткое решение (3–6 строк). Задачи должны требовать выписывания ОДЗ и отбора корней»

Как проверить:

ОДЗ должно быть явно выписано, разбор по случаям выполнен без пропусков, а все найденные корни проверены подстановкой. Это позволяет быстро понять, не пропустила ли модель условия корректности и не выдала ли формальный, но неверный ответ.

Планиметрия: углы и окружность

Мини-задача: «В окружности проведены касательная в точке A и хорда AB. Угол между ними равен 35°. Найдите величину дуги AB».

Если без визуала трудно, модель можно попросить схематично изобразить чертеж – это часто проясняет логику.

• Промпт для объясния решения по шагам: «Реши задачу про касательную и хорду. Опиши или нарисуй схему, сформулируй нужное свойство и поясни, почему оно применимо. Найди дугу AB и запиши ответ».
• Промпт для поиска поиска ошибки в решении: «Проверь мое решение задачи про касательную и хорду. Найди первый неверный шаг и исправь его. Мое решение: [текст]».
• Промпт для генерации 10 похожих задач: «Сгенерируй 10 задач уровня ЕГЭ на угол между касательной и хордой или подобие треугольников. Дай ответы и короткие решения».

Как проверить:

В планиметрии важно убедиться, что модель:

• Поняла, что дано и что требуется найти;
• Назвала и применила нужное свойство;
• Сформулировала решение так, чтобы чертеж был понятен даже без изображения.

Это помогает сразу увидеть логические разрывы и неправильно использованные теоремы.

Мы показали универсальную схему работы с нейросетью: разбор типовой задачи, поиск ошибок и генерация тренировочных упражнений. Этот формат одинаково работает для всех разделов математики. Поэтому дальше мы не повторяем промпты, а кратко разбираем типовые задачи других тем и показываем, как ИИ помогает избежать характерных ошибок.

Производная: исследование функции и экстремумы

Типовые задачи: возрастание/убывание, экстремумы, максимум/минимум на отрезке.

Где чаще всего ошибаются:

• Неверная производная;
• Пропущенные критические точки;
• Путаница со знаками производной;
• Игнорирование концов отрезка.

Как помогает ИИ:

• Проверяет корректность производной;
• Напоминает про анализ знаков;
• Контролирует проверку концов отрезка;
• Помогает оформить решение по алгоритму.

Как проверить:

При работе с производной в ответе модели стоит проверять корректность вычисления производной, полноту списка критических точек, верное определение знаков на промежутках и учет значений на концах отрезка. Такой алгоритм быстро выявляет наиболее частые ошибки ИИ при исследовании функций.

Интегралы: площадь и первообразная

Типовые задачи: определенный интеграл, площадь под графиком.

Где чаще всего ошибаются:

• Ошибка в первообразной;
• Механическая подстановка без смысла;
• Игнорирование отрицательных участков функции.

Как помогает ИИ:

• Проверяет первообразную;
• Связывает интеграл с графиком;
• Объясняет, где площадь вычитается;
• Помогает интерпретировать ответ.

Как проверить:

Проследите, что первообразная найдена корректно, пределы подставлены осмысленно, а знак площади учтен в соответствии с графиком функции. Это поможет избежать механических ошибок и понять, правильно ли интерпретирован результат.

Вероятность и комбинаторика: классика ЕГЭ

Типовые задачи: независимые события, «хотя бы одно», классические задачи на выбор объектов из группы (так называемые «урновые схемы»).

Где чаще всего ошибаются:

• Нверное пространство исходов;
• Путаница с независимостью;
• Неправильная формулировка случая;
• Забытый метод дополнения.

Как помогает ИИ:

• Переводит условие в формулы;
• Проверяет логику рассуждений;
• Показывает альтернативный способ;
• Выявляет логическую ошибку.

Как проверить:

Убидись, что пространство исходов сформировано верно, зависимость или независимость событий определена корректно, метод дополнения применен уместно, а формулировка каждого случая отражает условие задачи.

Стереометрия: объемы и углы

Типовые задачи: объемы тел, угол между прямой и плоскостью.

Где чаще всего ошибаются:

• Неверное построение;
• Путаница с высотой;
• Неправильная проекция;
• Ошибки в единицах.

Как помогает:

• Пошагово описывает построение;
• Помогает выбрать сечение;
• Может нарисовать схему;
• Контролирует формулы и размеры.

Как проверить:

Обратите внимание на правильность построения, выбор и понимание высоты, проекцию элементов и точность использования единиц измерения.

Олимпиадный уровень: неравенства и логика

Типовые задачи: неравенства (AM–GM – связь среднего арифметического и геометрического), задачи на логическое обоснование и базовая комбинаторика – подсчет числа возможных вариантов.

Где чаще всего ошибаются:

• Неверно выбран метод;
• Логические скачки;
• Забытые условия равенства;
• Нет проверки крайних случаев.

Как помогает ИИ:

• Проверяет логику доказательства;
• Обосновывает каждый переход;
• Предлагает альтернативный метод;
• Указывает слабые места.

Как проверить:

Четко ли определена цель рассуждений, обоснованы ли все переходы, указаны ли условия равенства и проверены ли граничные случаи? Ответьте на эти вопросы, чтобы быстро заметить слабые места в логике решения.

Нейросеть для решения задач по математике: тестируем популярные модели

Алгебра: модульное уравнение

Модель: GPT-5.2

Промпт:

«Реши задачу и объясни решение так, чтобы ученик мог воспроизвести на экзамене. Задача: "Решить уравнение |2x − 3| = x + 5". Требования к оформлению:

• Выпиши ОДЗ и поясни, почему оно такое;
• Реши по случаям (что внутри модуля ≥0 и <0), каждый шаг распиши;
• Каждый найденный корень проверь подстановкой в исходное уравнение;
• В конце дай короткое резюме: "какой метод и почему"».

Результат

GPT-5.2 решил задачу, не отклоняясь от заданной схемы.

Сначала нейросеть нашла область допустимых значений: из условия (|2x − 3|\ge 0) вывела (x + 5\ge 0), то есть (x\ge -5). Затем раскрыла модуль по случаям:

• (2x − 3\ge 0), что дало (x = 8);
• (2x – 3 < 0), что привело к (x = -\frac{2}{3}).

Каждое значение проверила на соответствие условию своего случая и ОДЗ. При подстановке корней все ответы сошлись. В конце ИИ кратко обозначил метод: уравнение с модулем решается, если разделить выражение на случаи в зависимости от знака подмодульного выражения.

А вот и само решение.

Алгебра: логарифмическое уравнение

Модель: Claude 4.5 Sonnet

Промпт:

«Реши уравнение и отдельно проверь ОДЗ. Задача: (\log_2(x − 1) + \log_2(x + 3) = 3). Формат:

1. ОДЗ (в виде системы неравенств).
2. Преобразование логарифмов с пояснением правила.
3. Решение полученного уравнения.
4. Отбор корней по ОДЗ и проверка.
5. Итог: ответ».

Результат

Модель:

• Выделила ОДЗ: (x > 1);
• Объединила логарифмы в один (\log_2[(x − 1)(x + 3)]);
• Привела уравнение к квадратному (x^2 + 2x – 11 = 0);
• Нашла корни (x = -1\pm2\sqrt3);
• Отбросила (x = -1-2\sqrt3) как нарушающий ОДЗ;
• Оставшийся корень (x = 2\sqrt3 - 1) проверила подстановкой.

Решение строго следует алгоритму. Каждое действие нейросеть объяснила. Просмотреть задачу можно тут.

Геометрия: угол между касательной и хордой

Модель: Gemini 3 Pro

Промпт:

«Реши геометрическую задачу. Если нужен рисунок, опиши его словами и введи обозначения. Задача: В окружности даны хорда AB и касательная в точке A. Угол между касательной и хордой AB равен 35°. Найди величину дуги AB (в градусах). Требования:

1. Сформулируй используемое свойство (угол между касательной и хордой).
2. Объясни, почему оно применимо.
3. Дай ответ и короткую проверку здравым смыслом (диапазон значений)».

Результат

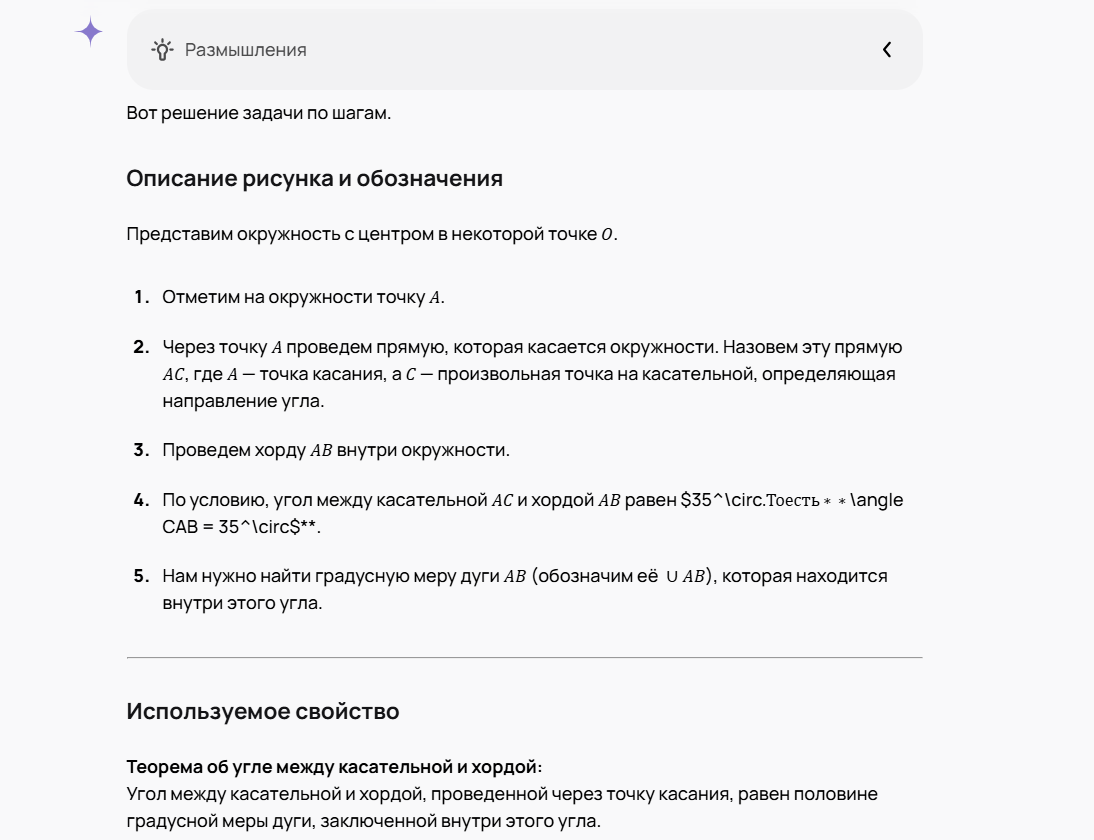
Gemini 3 Pro корректно применяет теорему о касательной и хорде: угол между ними равен половине дуги. Нейросеть:

• Подробно описала чертеж;
• Назвала свойство;
• Объяснила, почему оно подходит;
• Решила (35^\circ = \tfrac12x);
• Нашла (x = 70^\circ);
• Проверила результат с точки зрения логической обоснованности: острый угол дает дугу <90°, 70° подходит.

Решение структурированно и корректно. А ссылка на него – в этом диалоге.

Производная: исследование функции

Модель: Qwen 3 Max

Промпт:

«Исследуй функцию на отрезке и найди наибольшее значение. Задача: (f(x) = x^3 - 3x^2 - 9x + 1) на отрезке ([-1; 5]). Формат решения: производная → критические точки → таблица знаков → значения в критических и на концах → максимум. Обязательно: выпиши вычисления аккуратно, без "в уме"».

Результат

Qwen 3 Max:

• Вычислил производную (3x^2 - 6x - 9);
• Нашел критические точки (x = -1) и (x = 3);
• Составил таблицу знаков: функция растет при (x < -1) и (x > 3), убывает между ними;
• Рассчитал значения в точках (-1, 3, 5), получив (f(-1) = 6), (f(3) = -26), (f(5) = 6);
• Пришел к выводу, что наибольшее значение (6) достигается в концах интервала.

Решение произведено корректно и в рамках указанного алгоритма.

Сам пример – здесь.

Интегралы: вычисление и геометрический смысл

Модель: GPT-5.2

Промпт:

«Вычисли определенный интеграл и объясни, что он означает геометрически. Задача: (\int {0}^{2} (x^2+1), dx). Требования:

1. Найди первообразную с пояснением.
2. Подставь пределы, распиши арифметику.
3. Отдельно: что это за площадь и почему она положительная».

Результат

GPT-5.2 предоставил аккуратное и последовательное решение. Нейросеть:

• Разложила интеграл на (x^2) и (1);
• Объяснила формулы;
• Вывела первообразную (F(x) = x^3/3 + x);
• Вычислила (F(2) - F(0) = 14/3).

Затем пояснила, что интеграл – это площадь под графиком (y = x^2 + 1) между 0 и 2. Поскольку функция на отрезке всегда ≥1, площадь положительная.

Чтобы просмотреть решение, заходите сюда.

Вероятность

Модель: Claude 4.5 Sonnet

Промпт:

«Реши задачу по вероятности двумя способами, если возможно (прямой подсчет и через дополнение). Задача: "Монету подбрасывают 3 раза. Найди вероятность того, что орел выпадет хотя бы один раз". Формат:

1. Способ 1: через противоположное событие.
2. Способ 2: перечислением/биномиальной формулой (кратко).

Сверь ответы».

Результат

Claude 4.5 Sonnet четко показывает оба подхода. В первом нейросеть находит вероятность трех решек подряд (P(РРР) = 1/8) и вычисляет (P(\geq 1\ \text{орел}) = 1 - 1/8 = 7/8). Во втором перечисляет все восемь исходов, отмечает, что семь содержат орла, и снова получает (7/8).

В качестве альтернативы модель, как мы и просили, использует биномиальную формулу: (C_3^1 + C_3^2 + C_3^3 = 7) деленных на (2^3). Ответ совпадает – 0,875.

Оценить, как справился ИИ, можно тут.

Стереометрия: объем пирамиды

Модель: Qwen 3 Max

Промпт:

«Реши стереометрию, обозначения вводи явно. Задача: "Объем пирамиды равен 60. Площадь основания равна 24. Найди высоту пирамиды". Формат: формула объема → подстановка → решение → единицы измерения».

Результат

Здесь вычисления короткие, но модель четко выдерживает формат: сначала напоминает формулу (V = \tfrac{1}{3}S_\text{осн}h), затем подставляет (V = 60) и (S_\text{осн} = 24). Уравнение (60 = 8h) сводится к простому делению, и получается (h = 7{,}5). В ответе указаны единицы длины. Подход пошаговый, ясный, легко проследить, откуда берется число 7,5 и почему. А здесь – результат.

Олимпиадные неравенства

Модель: Claude 4.5 Sonnet

Промпт:

«Докажи неравенство, каждый переход поясняй. Задача: "Для (a > 0), (b > 0) докажи: (\frac{a}{b} + \frac{b}{a} ≥ 2)". Требования:

1. Укажи метод (AM–GM или ((a − b)^2 ≥ 0)) и почему он применим.
2. Пропиши условия равенства.
3. Дай краткий итог».

Результат

Модель выбирает неравенство AM–GM и подробно объясняет, почему его можно применить: (\frac{a}{b}) и (\frac{b}{a}) положительны. Она аккуратно пишет дроби, показывает, что их произведение равно 1, и после умножает обе части на 2, получая искомое неравенство.

После ИИ отмечает, что равенство возможно только при (a = b), так как только в этом случае (\frac{a}{b} = \frac{b}{a}). Пояснения изложены простым, доступным языком, оценить который вы можете в этом чате.

Заключение

Искусственный интеллект существенно ускоряет подготовку к экзаменам и олимпиадам. Он объясняет решения, помогает находить ошибки, служит в качестве генератора тренировочных задач. Но на экзамене решающее слово не за моделью, а за тем, кто ее использует: как человек понимает суть, может ли проверить область допустимых значений, не путается ли в условиях и формулах.

Чтобы получить необходимые навыки, действуйте по следующему алгоритму:

• Решите задачу.
• Сверьтесь с ИИ.
• Прочитайте разбор и комментарии от нейросети.
• Просите ее сгенерировать десяток аналогичных заданий.
• Проходите подобные циклы со следующими освоенными темами.

Такой подход поможет довести навыки до автоматизма, развить мышление, утвердиться в собственных знаниях. Таким образом, нейросеть для решения математики окажется не «последней соломинкой для утопающего», а надежным и безотказным онлайн-репетитором.